Curated OER
Past Continuous and Past Simple
In this verb forms worksheet, students complete a 20 question online interactive exercise pertaining to the correct use of the past continuous and past simple verb forms.
Curated OER
Complex Analysis: Complex Function
In this complex function worksheet students identify the derivative of given functions and explore the rules of differentiation. This two-page worksheet contains explanations and examples, followed by ten problems.
EngageNY
Why Stay with Whole Numbers?
Domain can be a tricky topic, especially when you relate it to context, but here is a instructional activity that provides concrete examples of discrete situations and those that are continuous. It also addresses where the input values...
EngageNY
Increasing and Decreasing Functions 2
Explore linear and nonlinear models to help your class build their function skills. In a continuation of the previous lesson, learners continue to analyze and sketch functions that model real-world situations. They progress from linear...
CK-12 Foundation
Function Rules for Input-Output Tables: Function Machine 1
Challenge your classes to find the pattern of a double function machine. After recording the outputs of both machines, learners identify the pattern and the corresponding function. Both patterns involve adding/subtracting a constant.
CK-12 Foundation
Function Rules for Input-Output Tables: Function Machine!
Watch as a function machine converts an input to an output. Learners determine the work applied by the function machine to write a function rule. Questions accompany the function machine animation to guide individuals to conclusions.
CK-12 Foundation
Horizontal and Vertical Asymptotes: Rational Functions
Play with the graph of a rational function to discover the asymptote patterns. Young scholars use the interactive lesson to discover the relationship between the asymptotes and the function. As they manipulate the function, the graph...
CK-12 Foundation
Graphs in the Coordinate Plane: Functions on a Cartesian Plane
Connect the dots to graph a linear function. Young mathematicians use an interactive to first plot provided points on a coordinate plane. They connect these points with a line and then answer questions about the slope and y-intercept of...
CK-12 Foundation
Logistic Functions: Fab Fitness
Strengthen your understanding of logistic functions. Young mathematicians change the carrying capacity of a logistic function and see how function values change. The function models the number of members in a gym over time.
CK-12 Foundation
Determining the Equation of a Line: Trip Functions
Let the function drive the activity. The interactive displays the odometer on a car for a trip. Pupils determine and interpret the slope of the situation. Then, they find a verbal description of the equation of the function.
CK-12 Foundation
Algebraic Functions: Vertical Line Test
To be (a function) or not to be (a function). An easy-to-use interactive has pupils drag a vertical line onto several graphs to determine if they represent functions. Some challenge questions assess understanding of this idea.
CK-12 Foundation
Infinite Limit Type: Evaluating Limits of Rational Functions
Rational functions become less mysterious when you know about limits. Individuals use an interactive to move a rational function on a coordinate plane and to investigate function values for certain x-values. They see how the limit...
CK-12 Foundation
Derivatives of Trigonometric Functions: Derivative of sin(x)
Graphically find the derivative of sin(x). Using the interactive, pupils graph the slope of the tangent line to the sine function. Class members use the resulting graph to determine the derivative of the sine function. They verify their...
EngageNY
Properties of Trigonometric Functions
Given a value of one trigonometric function, it is easy to determine others. Learners use the periodicity of trigonometric functions to develop properties. After studying the graphs of sine, cosine, and tangent, the lesson connects...
CK-12 Foundation
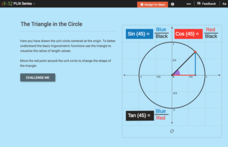
Trigonometric Functions and Angles of Rotation: The Triangle in the Circle
Go around the unit circle and create triangles. Pupils move a point around the unit circles to visualize the triangle associated with the angle in standard position. The three main trigonometric functions are defined in terms of the legs...
CK-12 Foundation
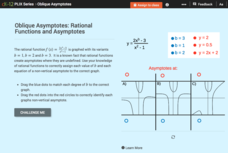
Oblique Asymptotes: Rational Functions and Asymptotes
Examine the connection between rational functions and their graphs. Individuals use an online manipulative to sort equations with horizontal and oblique asymptotes. They focus on the degree of the numerator and denominator.
CK-12 Foundation
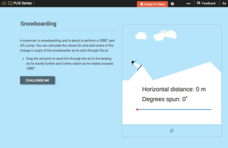
Trigonometric Functions of Angles Greater than 360 Degrees: Snowboarding
Spin through the trigonometric functions. Scholars determine the angle of rotation a snowboarding snowman makes at various distances in his jump. The class members then calculate the values of trigonometric functions for those angles.
CK-12 Foundation
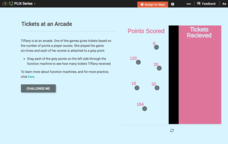
Function Rules for Input-Output Tables: Tickets at an Arcade
This is the ticket to learning about function rules! Using online manipulatives, scholars build a table of values and then answer questions about the related function. They examine the relationship between the input and output values and...
CK-12 Foundation
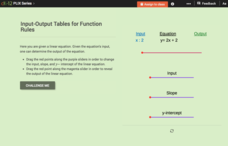
Input-Output Tables for Function Rules
How does changing a graph affect the function? Learners watch the changing input-output table as they adjust the location of the line graph. Questions prompt them to complete a table of values and determine the function rule.
CK-12 Foundation
Input-Output Tables for Function Rules
Make the abstract a bit more concrete with an interactive that asks learners to slide an input value through a function to determine the output. Changing the slope and y-intercept allows them to see the how the output values change.
CK-12 Foundation
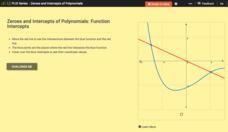
Zeroes and Intercepts of Polynomials: Function Intercepts
There is zero reason not to use the resource. Given a graph with a polynomial function and a linear function, scholars move the line in an interactive. To wrap up the lesson, they note how zeros and intersection points change.
Mt. San Antonio Collage
Quiz 1: Functions, Domain and Range
Take the work out of worksheets and use these problems and worked-out answer key as a resource. The problems reinforce skills in domain and range, identifying graphs, and even and odd functions.
EngageNY
Interpreting Quadratic Functions from Graphs and Tables
Seeing functions in nature is a beautiful part of mathematics by analyzing the motion of a dolphin over time. Then take a look at the value of a stock and maximize the profit of a new toy. Explore the application of quadratics by...
Code.org
One-way Functions – The WiFi Hotspot Problem
Pupils attempt to solve the Wireless Hotspot Problem and learn why it is considered a computationally hard problem in the ninth lesson of the series on 12. They also learn about one-way functions and how the Wireless Hotspot Problem is...