Flipped Math
Proving Lines Parallel
Show it can all be proved. Scholars learn the converses of the properties of parallel lines. Using the converses, pupils determine which lines are parallel based on angle measurements and practice using a flow proof to show that two...
EngageNY
Translating Lines
Define parallel lines through transformations. The third lesson of 18 examines the result of the translation of a line. Two possible outcomes include coinciding lines and parallel lines.
Academic Magnet High School
Parallel Lines Proofs Practice
Here is a worksheet that lines up perfectly with the skills needed to finish a geometric proof. Eleven problems are given to see if learners can prove that lines are parallel or angles are congruent.
Mathematics Assessment Project
Classifying Equations of Parallel and Perpendicular Lines
Parallel parking might be difficult, but finding parallel lines is fairly simple. In this lesson, learners first complete an assessment task involving parallel and perpendicular lines in the coordinate plane. Individuals then take part...
Mathematics Vision Project
Geometric Figures
Logical thinking is at the forefront of this jam-packed lesson, with young mathematicians not only investigating geometric concepts but also how they "know what they know". Through each activity and worksheet, learners wrestle with...
EngageNY
Looking More Carefully at Parallel Lines
Can you prove it? Making assumptions in geometry is commonplace. This resource requires mathematicians to prove the parallel line postulate through constructions. Learners construct parallel lines with a 180-degree rotation and then...
Geometry Accelerated
Accelerated Geometry Review Sheet
Your geometry learners use their knowledge of various geometric concepts to write proofs. Starting with givens containing parallel line segments with transversals and triangles and quadrilaterals, and the mid-point and distance formulas;...
Curated OER
Transformations in the Coordinate Plane
Your learners connect the new concepts of transformations in the coordinate plane to their previous knowledge using the solid vocabulary development in this unit. Like a foreign language, mathematics has its own set of vocabulary terms...
EngageNY
Comparing the Ratio Method with the Parallel Method
Can you prove it? Lead your class through the development of the Side Splitter Theorem through proofs. Individuals connect the ratio and parallel method of dilation through an exploration of two proofs. After completing the proofs,...
EngageNY
Informal Proofs of Properties of Dilations
Challenge the class to prove that the dilation properties always hold. The lesson develops an informal proof of the properties of dilations through a discussion. Two of the proofs are verified with each class member performing the...
EngageNY
Criterion for Perpendicularity
The Pythagorean Theorem is a geometry pupil's best friend! Learners explain the equation a1b1 + a2b2 = 0 for perpendicular segments using the Pythagorean Theorem. They are able to identify perpendicular segments using their...
EngageNY
Informal Proof of AA Criterion for Similarity
What does it take to show two triangles are similar? The 11th segment in a series of 16 introduces the AA Criterion for Similarity. A discussion provides an informal proof of the theorem. Exercises and problems require scholars to apply...
Inside Mathematics
Quadrilaterals
What figure is formed by connecting the midpoints of the sides of a quadrilateral? The geometry assessment task has class members work through the process of determining the figure inscribed in a quadrilateral. Pupils use geometric...
EngageNY
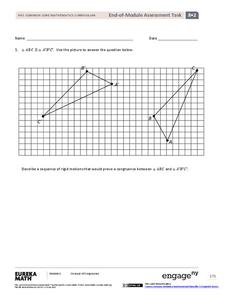
End-of-Module Assessment Task - Grade 8 Mathematics (Module 2)
Can your classes apply the knowledge they have learned? Use this performance task to find out! Individuals use transformations to explain congruence and angle relationships within parallel lines to find missing values. They show what...
Inside Mathematics
Circles in Triangles
Challenge the class with inscribed circles in triangles. The assessment task requests class members use their knowledge of circles and right triangles to prove two triangles are congruent. They go on to utilize their knowledge of...
EngageNY
Special Lines in Triangles (part 2)
Medians, midsegments, altitudes, oh my! Pupils study the properties of the median of a triangle, initially examining a proof utilizing midsegments to determine the length ratio of a median. They then use the information to find missing...
EngageNY
Special Lines in Triangles (part 1)
Allow your pupils to become the mathematicians! Individuals explore the properties of a midsegment of a triangle through construction and measurement. Once they figure out the properties, learners use them to draw conclusions.
Curated OER
Triangle's Interior Angles
Given a pair of parallel lines and a triangle in between, geometers prove that the sum of the interior angles is 180 degrees. This quick quest can be used as a pop quiz or exit ticket for your geometry class.
Mt. San Antonio Collage
The Trapezoid
Enjoy this nicely organized worksheet that puts together multiple problems regarding trapezoid proofs. The resource can be used as a guide that begins with proving properties and ends with solving for measures of line segments.
EngageNY
Angle Sum of a Triangle
Prove the Angle Sum Theorem of a triangle using parallel line and transversal angle relationships. Pupils create a triangle from parallel lines and transversals. They find angle measures to show that the angles of a triangle must total...
Illustrative Mathematics
Right Triangles Inscribed in Circles II
So many times the characteristics of triangles are presented as a vocabulary-type of lesson, but in this activity they are key to unraveling a proof. A unique attack on proving that an inscribed angle that subtends a diameter must be a...
Illustrative Mathematics
A Midpoint Miracle
Young geometers develop one of the fundamental properties of quadrilaterals (connecting side midpoints gives a parallelogram) in this short but thought-provoking exercise. Using a combination of hands-on techniques and abstract algebraic...
Illustrative Mathematics
What is a Trapezoid? (Part 1)
Challenge your class to construct a definition for trapezoids. Looking at four examples and four non-examples, students individually create definitions and use them to classify an unknown shape. Allow for small group and whole-class...
Mathematics Vision Project
Module 6: Congruence, Construction, and Proof
Trace the links between a variety of math concepts in this far-reaching unit. Ideas that seem very different on the outset (like the distance formula and rigid transformations) come together in very natural and logical ways. This...