CK-12 Foundation
Systems of Linear Equations in Three Variables: Intersecting Planes - No Solution
How many different ways can three planes intersect? The interactive provides three movable planes. Pupils manipulate the planes to determine the number of solutions possible based upon their intersections.
Kuta Software
Points in the Coordinate Plane
Keep young mathematicians on point with this coordinate plane worksheet. From plotting ordered pairs to identifying the quadrant and coordinates of specific points, this resource covers all the basic skills students need to have...
EngageNY
There is Only One Line Passing Through a Given Point with a Given Slope
Prove that an equation in slope-intercept form names only one line. At the beginning, the teacher leads the class through a proof that there is only one line passing through a given point with a given slope using contradiction. The 19th...
CK-12 Foundation
Zeroes and Intercepts of Polynomials: Function Intercepts
There is zero reason not to use the resource. Given a graph with a polynomial function and a linear function, scholars move the line in an interactive. To wrap up the lesson, they note how zeros and intersection points change.
Inside Mathematics
Graphs (2007)
Challenge the class to utilize their knowledge of linear and quadratic functions to determine the intersection of the parent quadratic graph and linear proportional graphs. Using the pattern for the solutions, individuals develop a...
Illustrative Mathematics
Fixing the Furnace
This comprehensive resource applies simultaneous equations to a real-life problem. Though the commentary starts with a graph, some home consumers may choose to begin with a table. A graph does aid learners to visualize the shift of one...
Concord Consortium
Shooting Arrows through a Hoop
The slope makes a difference. Given an equation of a circle and point, scholars determine the relationship of the slope of a line through the point and the number of intersections with the circle. After graphing the relationship, pupils...
McGraw Hill
Lines and Angles
Why was the obtuse angle upset? Because it was never right! A valuable resource is loaded with background information on types of angles and lines. Learners review the characteristics of parallel, perpendicular, and...
EngageNY
Segments That Meet at Right Angles
Can segments be considered perpendicular if they don't intersect? Learners look at nonintersecting segments on the coordinate plane and make conclusions about the lines that contain those segments. They determine if they are...
EngageNY
Geometric Interpretations of the Solutions of a Linear System
An intersection is more than just the point where lines intersect; explain this and the meaning of the intersection to your class. The 26th segment in a 33-part series uses graphing to solve systems of equations. Pupils graph linear...
EngageNY
Secant Lines; Secant Lines That Meet Inside a Circle
Young mathematicians identify different cases of intersecting secant lines. They then investigate the case where secant lines meet inside a circle.
EngageNY
Tangent Segments
What's so special about tangents? Learners first explore how if a circle is tangent to both rays of an angle, then its center is on the angle bisector. They then complete a set of exercises designed to explore further properties and...
EngageNY
Characterize Points on a Perpendicular Bisector
Learn transformations through constructions! Pupils use perpendicular bisectors to understand the movement of a reflection and rotation. They discover that the perpendicular bisector(s) determine the line of reflection and the...
CK-12 Foundation
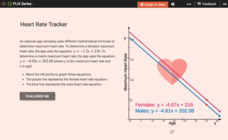
Graphs of Linear Systems: Heart Rate Tracker
Max out heart rates for males and females. Formulas of maximum heart rates provide the equations for a linear system. Pupils use the interactive to graph the equations for males and females and determine their points of intersection. The...
CK-12 Foundation
Graphs of Linear Systems: Star Lines
Let the class stars shine. Using four given linear equations, scholars create a graph of a star. The pupils use the interactive to graph the linear systems and determine the points of intersection. Through the activity, classmates...
Flipped Math
Graphing Functions to Solve Equations
Intersections become solutions. Scholars watch a video on using a graphing calculator to find the solution to an equation in one variable. While watching the presentation, pupils practice working some of the examples and compare their...
Radford University
Triangular Irrigation
Try to keep the pipe short. Learners investigate where to place a water pump to use the least amount of pipe. Scholars use their knowledge of reflections and congruent triangles to find the best location for the water pump. Finally, they...
Illustrative Mathematics
Global Positioning System II
Intricate details of a modern technology that many of us take for granted in our phones, computers (and some cars) are laid bare in a short but deeply investigative activity. The math behind a seemingly simple GPS device...
Inside Mathematics
Picking Apples
Getting the best pick of the apples depends on where to pick. The short assessment presents a situation in which class members must analyze a real-world situation to determine the cost of picking apples. The pricing structures resemble...
Illustrative Mathematics
Tangent to a Circle From a Point
Learners see application of construction techniques in a short but sophisticated problem. Combining the properties of inscribed triangles with tangent lines and radii makes a nice bridge between units, a way of using...
Regional Professional Development
Solving Systems of Equations by Graphing
With 30 problems, each accompanied by a blank graph, pupils get thorough practice solving systems of equations by graphing and finding the point of intersection. Answers are provided in coordinate form.
EngageNY
Lines That Pass Through Regions
Good things happen when algebra and geometry get together! Continue the exploration of coordinate geometry in the third lesson in the series. Pupils explore linear equations and describe the points of intersection with a given polygon as...
Concord Consortium
Look but Do Not Touch
We seem to keep missing each other. A short task provides pupils with a quadratic function, as well as a linear function with a missing coefficient. They must determine the value of the coefficient for which the graphs do not intersect.
Mathematics Vision Project
Circles: A Geometric Perspective
Circles are the foundation of many geometric concepts and extensions - a point that is thoroughly driven home in this extensive unit. Fundamental properties of circles are investigated (including sector area, angle measure, and...