Bowland
Geoboard Squares
Don't be a square! Help your budding mathematicians discover patterns within squares. Scholars create squares on geoboards and identify patterns in the number of nails, both nails on the edge of the squares and nails within the squares....
Bowland
Problem Page
Future mathematicians use a given graph to answer a question about age differences in relationships. Along the way, they must find the equation and inequality of given graphs.
Bowland
Soft Drinks
"Statistics are no substitute for judgment" - Henry Clay. Young mathematicians use provided statistics from a soda taste test to explain why conclusions are faulty. They devise a new test that would be more appropriate than the one given.
Math Warehouse
Theoretical Probability Activity
If you keep rolling a die, you'll roll a five exactly one-sixth of the time—right? A probability lesson prompts young mathematicians to roll a die 100 times and use the data to calculate empirical probabilities. They then compare...
Bowland
The Z Factor
Young mathematicians determine the number of hours it would take judges of the "Z Factor" television talent show to watch every act. Participants make estimates and assumptions to solve the problem.
Bowland
Design the Mascot
Explore how resizing an object affects its area. The set of lessons challenges young mathematicians to design a mascot for electronic devices. These designs undergo resizing to determine how scale factors of dilation affect area.
Education Development Center
Micro-Geography of the Number Line
Young mathematicians dive into the number line to discover decimals and how the numbers infinitely get smaller in between. They click the zoom button a few times and learn that the number line doesn't just stop at integers. Includes...
Mathed Up!
Standard Form
Be sure your young mathematicians can work with scientific notation. Scholars first watch a video to review scientific notation. They then complete a activity requiring conversions and operations with scientific notation.
Mathed Up!
Frequency Polygons
Frequency polygons are a different way to represent frequencies over intervals. Pupils take frequencies for intervals of data from a frequency table and plot them as a frequency polygon. Budding mathematicians find information about the...
Mathed Up!
Stratified Sampling
Young mathematicians learn how to solve problems involving stratified sampling. They review concepts of sampling and proportionality by watching a video and then they complete a worksheet of questions on this topic.
CK-12 Foundation
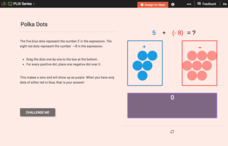
Addition of Integers: Polka Dots
What happens when you add negative and positive integers to one another? Do you add or subtract, and will the answer be positive or negative? Young mathematicians use blue and red polka dots to determine the value of an expression that...
CK-12 Foundation
Percent of a Number: Rock Climbing
What percent of the 100 ft. rock has Marta climbed? Young mathematicians find the percent of number (the rock height) by moving the climber up and down the rock.
CK-12 Foundation
Slope-Intercept Form: Mountain Train
Hop aboard to learn about the slope-intercept form. Young mathematicians use an interactive to adjust the path a train takes up a mountain. A set of challenge questions helps them see the connection between key features and the...
CK-12 Foundation
Definition of Probability: It's in the Bag!
It's not in the bag. An interactive provides the probability of picking a certain color marble from a bag after several marbles have been removed. Young mathematicians learn about dependent events from this resource.
CK-12 Foundation
Measurement of Probability: Basketball Throw
Future mathematicians use an interactive to see how changing the size of a basketball court and the size of a region in the court affects the probability that a ball will randomly fall within the specified region. No calculations are...
CK-12 Foundation
Basic Counting Rules: Sandwich Shop
Young mathematicians make a tree diagram of all possibilities for sandwiches using an interactive. They learn how multiplication speeds up the process of finding the number of outcomes.
CK-12 Foundation
Graphs Using Slope-Intercept Form: Zip-Line
Zip lines aren't so scary when all your scholars use them for is math. Young mathematicians see how the slope of a zip-line to a building changes as the height changes. They answer a set of challenge questions regarding the scenario.
CK-12 Foundation
Graphs in the Coordinate Plane: Functions on a Cartesian Plane
Connect the dots to graph a linear function. Young mathematicians use an interactive to first plot provided points on a coordinate plane. They connect these points with a line and then answer questions about the slope and y-intercept of...
CK-12 Foundation
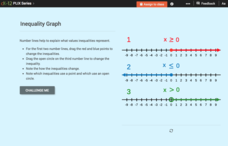
Inequality Expressions: Inequality Graph
Don't let inequalities be a drag. As young mathematicians drag the endpoint of the graph of an inequality in an interactive, the algebraic form of the inequality changes. This helps them see how the graph connects to the inequality.
CK-12 Foundation
Two-Step Equations with Subtraction and Multiplication: Cupcake Equation
Solving equations is a piece of cake. Young mathematicians use an interactive to create a bar model to representing a situation involving cupcakes. They use the model to solve for the cost of a cupcake.
CK-12 Foundation
Complementary Angles: Corner Kick
Soccer is all about angles. Young mathematicians use an interactive to correctly position the path of a soccer ball so that it reaches the goal. They consider complementary angles when answering a set of challenge questions.
CK-12 Foundation
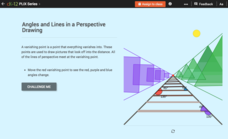
Linear Pairs: Angles and Lines in a Perspective Drawing
Gain some perspective on linear pairs. Aspiring mathematicians adjust the vanishing point on a perspective drawing. They see the effect on linear pairs of angles and answer five challenge questions based on their observations.
CK-12 Foundation
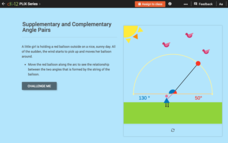
Supplementary and Complementary Angle Pairs
Complement and supplement your knowledge of angles. Young mathematicians study supplementary and complementary angle pairs using an interactive. A set of challenge questions solidifies this understanding.
CK-12 Foundation
Converse, Inverse, and Contrapositive
Logically speaking, here is a great resource. Young mathematicians apply an interactive to consider the converse, inverse and contrapositive statements. Eight challenge questions assess understanding of the material.
Other popular searches
- Famous Mathematicians
- Great Mathematicians
- 5 Great Mathematicians
- Female Mathematicians
- Projects on Mathematicians
- Five Great Mathematicians
- The Great Mathematicians
- Mathematicians Fibonacci
- List of Great Mathematicians
- Hall of Great Mathematicians
- Whorls Famous Mathematicians
- The Old Grete Mathematicians