Curated OER
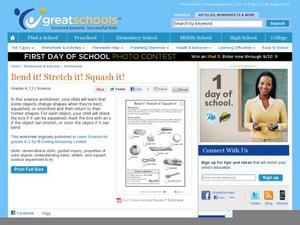
Bend It! Stretch It! Squash It!
Some items keep their shape no matter what happens! Have your kindergarten class choose which items would stay the same if they were bent, stretched, or squashed. The last activity prompts kids to see what happens when they stretch a...
Curated OER
Growing
Growing is part of being a living thing. Kindergartners decide which illustrations represent the life cycle of a living thing, then put a check mark next to the correct pictures. They then examine their own growth on a height chart.
Curated OER
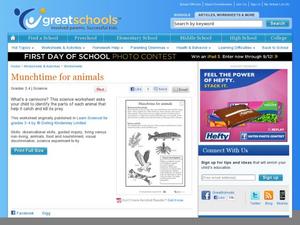
Munchtime for animals
Which animals eat meat to stay alive? Third graders group fish, hawks, and cats into carnivores and herbivores. An extended activity prompts kids to cut out magazine pictures of different animals according to the foods that they eat.
Curated OER
Exponential Reflections
High Schoolers explore the concept of exponential reflections. They use their Ti-Nspire to reflect the natural logarithm function over the line y=x. Students repeat the process using different exponential functions using a slider.
Curated OER
Going Back to Your Roots
Investigate the Fundamental Theorem of Algebra and explore polynomial equations to determine the number of factors, the number of roots, and investigate multiplicity of roots.
Curated OER
Ring-A-Ding-Ding!
What sound does metal make when you hit it? Kindergartners and first graders conduct an experiment about the properties of metal. First, they draw a line between metal items and descriptions of each. Next, they use a magnet to see which...
DK Publishing
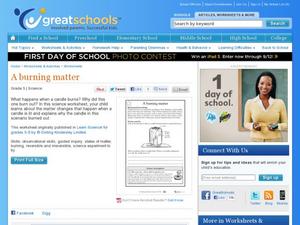
A Burning Matter
The process of fire requires oxygen, heat, and fuel. Take one of those away, and fire ceases to exist. That's the idea behind this instructional activity which portrays a candle burning inside an upside down jar. Pupils answer a couple...
Curated OER
Critical Thinking Problems
Young mathematicians practice their reasoning as well as adding and subtracting skills with this worksheet that includes five simple word problems about birthdays. Learners are give pictures of birthday cakes and based on the number of...
Education Development Center
Absolute Value Reasoning
Teach solving absolute value inequalities through inquiry. Groups use their knowledge of absolute value and solving inequalities to find a solution set to an absolute value inequality. Working collaboratively encourages discussion,...
Education Development Center
Comparing Fractions
Three heads are better than one. After reading a conversation between three friends about how to compare fractions, scholars analyze and discuss each presented strategy. These include using unit fractions, using benchmark fractions,...
Computer Science Unplugged
Count the Dots – Binary Numbers
Did you know you can send a message using only zeroes and ones? This interactive resource presents an introduction to binary numbers. Through code cards, pupils learn to convert binary numbers to decimal numbers.
Curated OER
How Does Water Cool?
How fast does water cool? First fifth graders will draw a line on a graph that predicts how fast they think water can cool from boiling. Then they plot the actual data on the same graph to see if their estimate was correct.
Education Development Center
Points, Slopes, and Lines
Before graphing and finding distances, learners investigate the coordinate plane and look at patterns related to plotted points. Points are plotted and the goal is to look at the horizontal and vertical distances between coordinates and...
Education Development Center
Making Sense of Unusual Results
Collaboration is the key for this equation-solving lesson. Learners solve a multi-step linear equation that requires using the distributive property. Within collaborative groups, scholars discuss multiple methods and troubleshoot mistakes.
Education Development Center
Interpreting Statistical Measures—Class Scores
Explore the effect of outliers through an analysis of mean, median, and standard deviation. Your classes examine and compare these measures for two groups. They must make sense of a group that has a higher mean but lower median compared...
Education Development Center
Creating a Polynomial Function to Fit a Table
Discover relationships between linear and nonlinear functions. Initially, a set of data seems linear, but upon further exploration, pupils realize the data can model an infinite number of functions. Scholars use multiple representations...
Education Development Center
Integer Combinations—Postage Stamps Problem (MS Version)
Number patterns can seem mysterious. Help your learners unravel these mysteries as they complete an intriguing task. Through examination, collaborative groups determine that they are able to produce all integers above a certain...
Education Development Center
Consecutive Sums
Evaluate patterns of numbers through an engaging task. Scholars work collaboratively to determine a general rule reflecting the sum of consecutive positive integers. Multiple patterns emerge as learners explore different arrangements.
Education Development Center
Choosing Samples
What makes a good sample? Your classes collaborate to answer this question through a task involving areas of rectangles. Given a set of 100 rectangles, they sample a set of five rectangles to estimate the average area of the figures. The...
Education Development Center
Proof with Parallelogram Vertices
Geometric figures are perfect to use for proofs. Scholars prove conjectures about whether given points lie on a triangle and about midpoints. They use a provided dialogue among fictional students to frame their responses.
Education Development Center
Rational Exponents
It's rational to root for your class to learn about exponents. Scholars study rational exponents by reading a fictional dialogue between classmates. They analyze the conversation to understand the connection between rational exponents...
Education Development Center
Extending Patterns with Exponents
Don't think negatively about exponents. Young mathematicians dissect a fictional conversation between pupils trying to evaluate an expression with a negative exponent. This allows them to understand the meaning of negative exponents.
Education Development Center
Sum of Rational and Irrational is Irrational
Sometimes the indirect path is best. Scholars determine whether the sum of a rational number and an irrational number is irrational. Reading a transcript of a conversation between classmates leads to an indirect proof of this concept.