EngageNY
Arcs and Chords
You've investigated relationships between chords, radii, and diameters—now it's time for arcs. Learners investigate relationships between arcs and chords. Learners then prove that congruent chords have congruent arcs, congruent arcs have...
Curated OER
Properties of Arcs, Lengths and Chords
Young scholars differentiate between the different properties of arcs, arc lengths, chords, and chord lengths. In this circles lesson, students calculate the arc length of a given circle, and find the measure of the inscribed angles of a...
Virginia Department of Education
Angles, Arcs, and Segments in Circles
Investigate relationships between angles, arcs, and segments in circles. Pupils use geometry software to discover the relationships between angles, arcs, and segments associated with circles. Class members use similar triangles to...
Virginia Department of Education
Arc Length and Area of a Sector
What do skateboarding and baked goods have in common with math? You can use them to connect half-pipe ramps and cakes to arcs and sectors. Pupils compare the lengths of three different ramp options of a skate park. They calculate the...
Curated OER
Circles and Angles
Students identify tangents, chords and secants. In this geometry activity, students graph circles and identify angles created by secant lines, tangent lines and chords.
Curated OER
Looking at Circumference
Students understand where the number for pi comes from. They understand and use the formula for circumference. Students measure the circles given out and the diameters of those circles and record the results on their worksheet.
EngageNY
Rectangles Inscribed in Circles
Putting a rectangular object into a circular one—didn't the astronauts on Apollo 13 have to do something like this? Learners first construct the center of a circle using perpendiculars. They then discover how to inscribe a rectangle in a...
Curated OER
Equations of Circles
Students will define circle and radius. In this radius lesson, students are given a circumference, they will write an equation and sketch the circle. Students will match graphs of circles to their equations.
Curated OER
Chords of a Circle
In this geometry worksheet, 10th graders calculate the length of a chord and the distance from the center of a circle or radius. They compare diameter, chords and radius. There are 10 questions with an answer key.
Curated OER
Circle Packing
Learners identify different parts and properties of circles. In this geometry lesson, students identify the radius, diameter, semicircle and inscribed angle of a circle. They identify the tangent lines to a circle.
Curated OER
Circles
Tenth graders explore and define the radius and diameter of a circle. In this geometry instructional activity, 10th graders calculate the circumference and area of a circle using real world objects and shapes. They discuss chords...
Curated OER
Chors, Secants, Tangents
Students identify the relationship between chords, secants and circles. In this geometry lesson, students calculate the length of the chords. They sketch the secant lines on a circle.
Curated OER
Tangent Properties
Students explore properties of tangent lines. In this properties of tangent lines lesson, students discuss the perpendicular relationship between a tangent line on a circle and the circle's radius. Students use that...
Curated OER
Where in the World
Students explore the global grid system. In this globe lesson, students identify latitude and longitude lines and how these can tell the coordinates of any place. They use the Internet to find the exact coordinates for their town.
Curated OER
Parts of a Circle
Sixth graders use yarn, paper plate, and other materials to identify parts of a circle. In this parts of a circle lesson plan, 6th graders identify the circumference, radius, diameter, and other parts of a circle.
Curated OER
Sir Cumference and the Dragon Pi
Geometry adventurers study circumference of a circle as they listen to Sir Circumference and the Dragon Pi, by Cindy Neuschwander. In groups, they use string to measure the diameter and circumference of circular objects and...
Curated OER
Geometry of Circles - Week 7 (Area & Circumference)
In this circle worksheet, students solve problems involving the circumference, area and arc length in a circle. They explore the union of circles and semicircles, as well as the line segments tangent to the circle. This two-page...
Curated OER
Searching The Word
Fifth graders review EOG math terms and definitions found in their math notebooks, and pick between 15 and 20 words to put in a word search.
Curated OER
Using Circumference
Young scholars participate in a lesson that covers the concept of finding the circumference of a circle. The teacher covers relevant vocabulary with the students. They work in groups to measure objects and calculate the formula to find...
Curated OER
Inscribed Angles
Students analyze inscribed angles and intercepted arcs and explore the relationships between the two. They investigate the properties of angles, arcs, chords, tangents, and secants to solve problems involving circles.
Curated OER
Geometry of Circles: Week 7
In this circle worksheet, students determine the number of degrees in a minor arc, find the area of a circle, find the area of a shaded region. This two-page worksheet contains six problems.
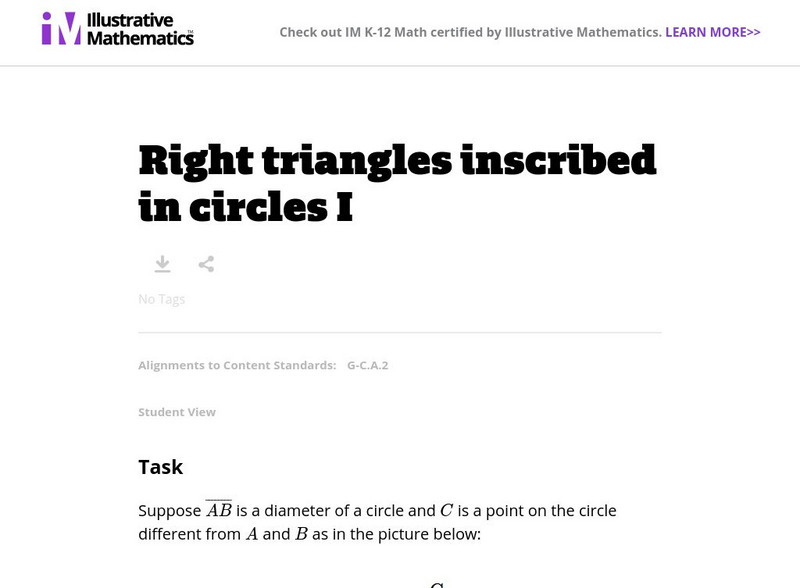
Illustrative Mathematics
Illustrative Mathematics: G C Right Triangles Inscribed in Circles I
This task provides a good opportunity to use isosceles triangles and their properties to show an interesting and important result about triangles inscribed in a circle with one side of the triangle a diameter. The fact that these...
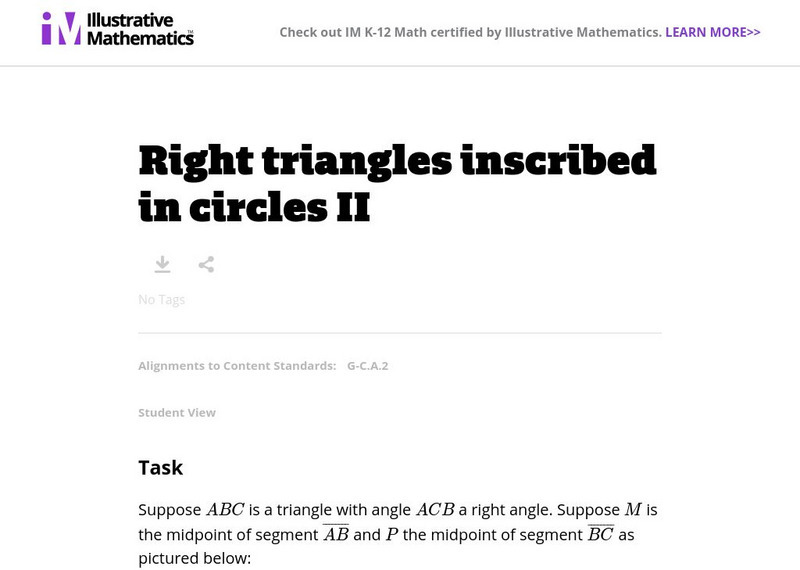
Illustrative Mathematics
Illustrative Mathematics: G C Right Triangles Inscribed in Circles Ii
For this task, students analyze the characteristics of a right triangle that has two sides labeled with midpoints and show that the triangle is inscribed in a circle with a diameter the length of its hypotenuse. Aligns with G-C.A.2.
Alabama Learning Exchange
Alex: Talking in Circles
The students will identify parts of the circle including center, radius, diameter, chord, and arc. This lesson plan was created by exemplary Alabama Math Teachers through the AMSTI project.