Illustrative Mathematics
Illustrative Mathematics: G Mg Hexagonal Pattern of Beehives
Beehives are made of walls, each of the same size, enclosing small hexagonal cells where honey and pollen are stored and bees are raised. This problem examines some of the mathematical advantages of the hexagonal tiling in a beehive....
Illustrative Mathematics
Illustrative Mathematics: G Mg Toilet Roll
Picture a roll of toilet paper; assume that the paper in the roll is very tightly rolled. Assuming that the paper in the roll is very thin, find a relationship between the thickness of the paper, the inner and outer radii of the roll,...
Illustrative Mathematics
Illustrative Mathematics: G Mg How Many Cells Are in the Human Body?
About how many cells are in the human body? The purpose of this task is for students to apply the concepts of mass, volume, and density in a real-world context. Aligns with G-MG.A.2.
Illustrative Mathematics
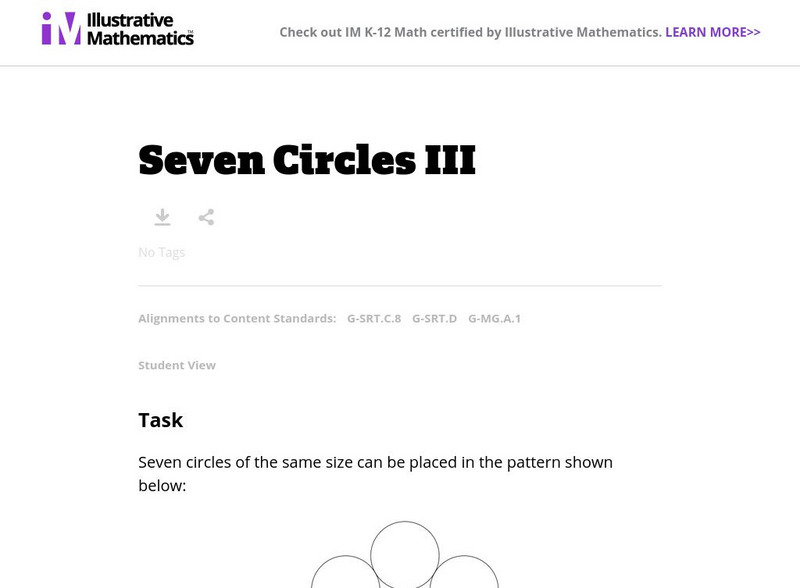
Illustrative Mathematics: G Srt, G Mg Seven Circles Iii
In this task, students are shown circle formations where an inner circle is surrounded by a set of circles and all circles are touching. In the first situation, all circles have the same diameter. In the second, the inner circle is...
Illustrative Mathematics
Illustrative Mathematics: G Mg, G Gmd Global Positioning System Ii
Satellites communicate with a GPS device and establish the distance between them and their locations. The set of points at a fixed distance from a satellite form a sphere so when the GPS receives its distance from a given satellite, this...
Illustrative Mathematics
Illustrative Mathematics: G Mg How Thick Is a Soda Can? Variation I
In this task, students are given the dimensions of a soda can and are asked to estimate its thickness. They must first find the surface area and the volume of aluminum. Aligns with G-MG.A.1 and G-MG.A.2.
Illustrative Mathematics
Illustrative Mathematics: G Mg Tilt of Earth's Axis and the Four Seasons
This task gives students a chance to explore the effects of the Earth's tilt and rotation using a simple geometric model of Earth-Sun interaction that shows why the seasons occur. Aligns with G-MG.A.1.