Dartmouth College
Dartmouth College: The Different Styles of Euclid and Copernicus
A history of the differences between Euclid's and Copernicus's methods of proving geometric ideas.
University of Canterbury
Canterbury: The Konigsberg Bridge Problem
An introduction to the Konigsberg Bridge problem and its relationship to network theory.
Other
Polyhedra: The Five Platonic Solids
A brief site that includes some activities to understand the figures.
Cut the Knot
Cut the Knot!: The Law of Cosines (Cosine Rule)
This site from Cut The Knot provides an overview of the law of cosines, complete with an explanation of the law and a proof of the law.
University of Massachusetts
Fractal Project: Exploring Fractals
A good beginner's site for fractals - the language is straightforward and requires only minimal experience to be able to understand the topic. (Note: When clicking on links on archived site, they may pause and appear not to be found...
Math Open Reference
Math Open Reference: Constructions
Learn about drawing shapes using only a compass and straight edge or ruler with out measuring any lengths or angles.
Other
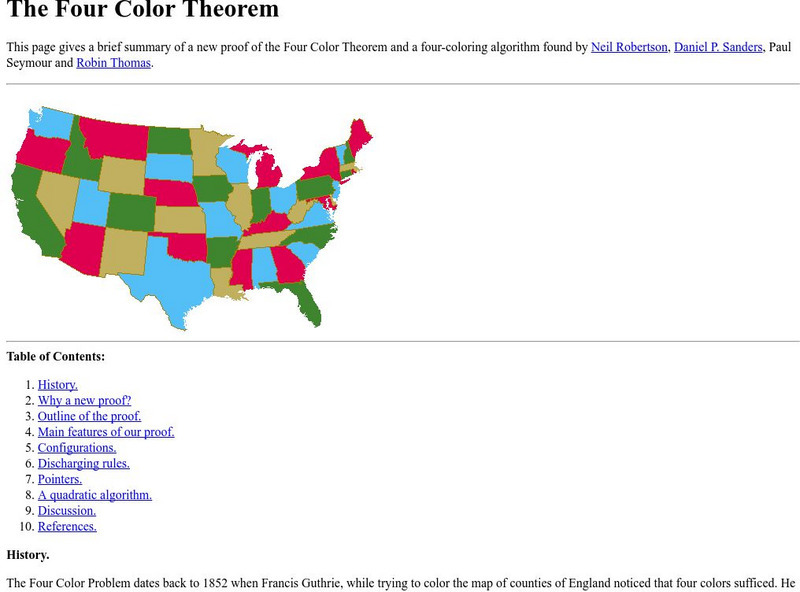
Georgia Tech: The Four Color Theorem
An explanation and proof of the Four Color Map Theorem. Includes illustrative images and a plethora of information.
University of St. Andrews (UK)
University of St. Andrews: St. Andrews: History of the Four Color Theorem
The University of St. Andrews offers a brief history of the first math problem to be solved with computers.
Boston University
Boston University: Chaos, Fractals and Arcadia
This is an interesting site for information on chaos and fractals. Includes links to interactive activities to learn more.
Shodor Education Foundation
Shodor Interactivate: Lesson: Fractals
This site provides some links to activities and lesson plans dealing with fractals and chaos.
Other
Mathematical the Four Color Theorem and Computer Proof
This site describes the role of computer involvement in the four color map theorem.
Other
Eal: Fract Ed
A great resource for beginners. The site begins with a definition of iteration of functions, and proceeds from there to discuss fractal dimension.