Brian McLogan
Find the missing value using two secant lines from a point outside of the circle
Learn how to solve problems with secant lines. A secant line is a line that intersects a circle at exactly 2 points in contrast to a tangent line which is a line that touches a circle at exactly one point. When two secant lines...
Brian McLogan
Learn to find the average acceraltion of a particle not given in a table
👉 Learn how to solve particle motion problems. Particle motion problems are usually modeled using functions. Now, when the function modeling the position of the particle is given with respect to the time, we find the speed function of...
Brian McLogan
Determine the derivative expanding a binomial to use the power rule
👉 Learn how to find the derivative of a function using the power rule. The derivative of a function, y = f(x), is the measure of the rate of change of the function, y, with respect to the variable x. The process of finding the derivative...
Brian McLogan
Using triangles to evaluate for the difference formula of tangent
👉 Learn how to evaluate the secant of the sum or difference of two angles using the sum/difference formulas. To do this, we first use the Pythagoras theorem to obtain all the sides of the right triangle in the unit circle. Recall that...
Math Fortress
Calculus I: Derivatives of Polynomials and Natural Exponential Functions (Level 1 of 3)
This video will teach you the basics of calculating the derivative of simple polynomials and exponential functions.
Brian McLogan
Find the value of x given a tangent line to a circle
Learn how to solve problems with tangent line. A tangent line to a circle is a line that touches the circle at exactly one point. The tangent line to a circle makes a right angle with the radius of the circle at the point of its...
Professor Dave Explains
Derivatives of Trigonometric Functions
How to take the derivatives of trigonometric functions.
Catalyst University
Titration Curves: A Conceptual Math-based Approach
Titration Curves: A Conceptual Math-based Approach
Curated Video
Properties of Circles: Tangents and Perpendicularity
In this video, the teacher explains the concept of tangents to a circle and their relationship with the radius. The teacher proves the theorem that a tangent line is perpendicular to the radius at the point of tangency. Additionally, the...
Professor Dave Explains
Understanding Differentiation Part 2: Rates of Change
Conceptualizing differentiation using the rates of change.
Brian McLogan
Given a point outside a circle and a tangent line determine the length from the point to center
Learn how to solve problems with tangent line. A tangent line to a circle is a line that touches the circle at exactly one point. The tangent line to a circle makes a right angle with the radius of the circle at the point of its...
Professor Dave Explains
Finding Local Maxima and Minima by Differentiation
How to find the local maxima and minima of a function using differentiation.
Professor Dave Explains
Understanding Differentiation Part 1: The Slope of a Tangent Line
Conceptualizing differentiation using the slope of a tangent line.
Professor Dave Explains
The Mean Value Theorem For Integrals: Average Value of a Function
Defining the mean value theorem for integrals.
Virtually Passed
Math Puzzle - How many circles wrap around a circle?
How many circles, N, of radii r can be wrapped around a circle of radius R? What is the value of r/R when N=3?
Professor Dave Explains
Graphing Functions and Their Derivatives
How to graph functions and their derivatives.
Brian McLogan
How to determine the value of x using the definition of a tangent line to a circle
Learn how to solve problems with tangent line. A tangent line to a circle is a line that touches the circle at exactly one point. The tangent line to a circle makes a right angle with the radius of the circle at the point of its...
Schooling Online
Physics Kinematics: Motion in a Straight Line - Distance-Time and Displacement-Time Graphs
Mark Brent’s coffee run takes a turn for the worse when he has a nasty encounter with Negative Nancy! This lesson will discover the importance of distance-time graphs and displacement-time graphs for representing motion.
Definitions...
Professor Dave Explains
Position/Velocity/Acceleration Part 2: Graphical Analysis
Everyone loves graphs! Especially when they give us so much information about the motion of an object. Position, velocity, and acceleration can be plotted against time, and these curves all relate to one another in interesting ways....
Professor Dave Explains
What is a Derivative? Deriving the Power Rule
What is it to take the derivative of a function? Let's derive and define the power rule, so that we can take the derivative of simple polynomials.
Professor Dave Explains
Uniform Circular Motion and Centripetal Force
Enough of this moving in straight lines business, let's go in circles! It may not be productive but it's super fun. Ferris wheels are fun. Yes they are, don't be a spoilsport. Roller coasters are fun too. And merry-go-rounds. Look, I...
Khan Academy
Equation of a Tangent Line, Taking Derivatives, Differential Calculus
Using a specific example, Sal shows how to find the equation of a tangent line to a given function at a specific point. Specifically, he solves the problem of finding the tangent line to the function f(x) = xex at x = 1. This problem...
Khan Academy
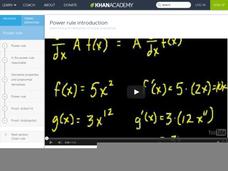
Power Rule Introduction (Old) Taking derivatives, Differential Calculus
This video covers the differential notation dy/dx and generalizes the rule for finding the derivative of any polynomial. It also extends the notion of the derivatives covered in the Khan Academy videos, "Calculus Derivatives 2Ó and...
Khan Academy
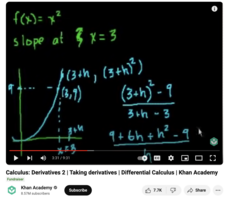
Calculus: Derivatives 2
Sal continues where he left off with the last video, "Derivatives 1, Ó by looking at the equation y = x^2 and examining the slope of the second line at a specific point, and again defining the limit as x approaches zero to get the slope...